Rumus Persamaan Garis Lurus Dan Penjelasannya
Posted on 02 05 2019
Persamaan Garis Lurus | Persamaan garis lurus adalah salah satu cabang ilmu matematika yang dipelajari sejak kita duduk di bangku SMP . Sebenarnya apakah yang dimaksud dengan persamaan garis lurus ? dan bagaimanakah rumus – rumusnya ?
Persamaan garis lurus dapat diartikan juga dengan persamaan linier yaitu ada yang teriri dari satu variabel dan ada juga yang terdiri dari dua variabel . Untuk lebih jelasnya , perhatikan penjelasan – pejelasan di bawah ini .
Rumus Persamaan Garis Lurus
Sebelum kita mempelajari tentang rumus – rumus persamaan garis lurus , kita harus memahami terlebih dahulu pengertian dari persamaan garis lurus itu sendiri .Dan dalam sebuah persamaan garis lurus.
Ada satu komponen yang tidak dapat terlepas darinya yaitu Gradien . Apakah yang dimaksud dengan gradien? Perhaikan penjelasan di bawah ini :
A. Pengertian Persamaan Garis Lurus Dan Gradien
Persamaan Garis lurus , yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis .
Gradien , yaitu Perbandingan komponen y dan komponen x , atau disebut juga dengan kecondongan sebuah garis. Lambang dari suatu gradien yaitu huruf “m” .
- Gradien dari persamaan ax + by + c = 0
- Gradien yang melalui titik pusat ( 0 , 0 ) dan titik ( a , b )
m = b/a
- Gradien Yang melalui titik ( x1 , y 1 ) dan ( x2 , y2 )
m = y1 – y2 / x1 – x2 atau m = y2 – y1 / x2 – x1
- Gradien garis yang saling sejajar ( / / )
m = sama atau jika dilambangkan adalah m1 = m2
- Gradien garis yang saling tegak lurus ( lawan dan kebalikan )
m = -1 atau m1 x m2 = -1
B. Rumus Persamaan Garis Lurus
1. Persamaan Garis Lurus bentuk umum ( y = mx )
-> persamaan yang melalui titik pusat ( 0 , 0 ) dan bergradien m .
Contoh :
Tentukan persamaan garis lurus yang melalui titik pusat ( 0 , 0 ) dan bergradien 2 !
Jawab : y = mx
y = 2 x
2. y = mx + c
->Persamaan garis yang / / dengan y = mx dan bergradien m
-> Persamaan garis yang melalui titik ( 0 , c ) dan bergradien m. ( 0 , c ) adalah titik potong sumbu y .
3. Persamaan Garis Lurus Yang Melalui titik ( x1 , y1 ) dan bergradien m .
persamaannya yaitu :
y – y1 = m ( x – x1 )
4. Persamaan Garis Lurus Yang Melaui Dua titik yaitu ( x1 , y 1 ) dan ( x2 , y2 ) .
Contoh Soal Persamaan Garis Lurus
Contoh Soal 1Tentukan Gradien garis yang melalui titik ( 0 , 0 ) dengan titik A ( -20 , 25 ) ?
Penyelesaian :
Diketahui :Titik ( 0 , 0 )
Titik A ( -20 , 25 )
Ditanya : m = . . .?
Jawab :m = b / a = 25 / -20 = – 5/4
Contoh Soal 2Tentukan Gradien garis yang melalui titik A ( -4 , 7 ) dan B ( 2 , -2 ) ?
Penyelesaian :
Diketahui :
Titik A ( -4 , 7 )
TitikB ( 2 , -2 )
Titik A ( -4 , 7 )
TitikB ( 2 , -2 )
Ditanya : m = . . ?
Jawab :m= y1 – y2 / x1 – x2
m = 7 – ( -2) / -4 -2
m = 9 / -6
m = – 3/2
m = 7 – ( -2) / -4 -2
m = 9 / -6
m = – 3/2
Tentukan Gradien garis dengan persamaan garis 4x + 5y – 6 = 0 ?
Penyelesaian :
Diketahui :
Persamaan 4x + 5y – 6 = 0
Persamaan 4x + 5y – 6 = 0
Ditanya : m = . . .?
Jawab :m = -a / bm = -4 / 5
Contoh Soal 4
Tentukan persamaan garis lurus yang melalui pusat koordinat dan bergradien – 4/5 ?
Penyelesaian :
Diketahui :
Titik pusat koordinat ( 0 , 0 )
m = -4/5
Titik pusat koordinat ( 0 , 0 )
m = -4/5
Ditanya : Persamaan garis lurus = . . .?
Jawab :
y = mx
y = -4 / 5 x
-4y = 5x
-4y -5y = 0
<-> 4y + 5y = 0
Contoh Soal 5y = mx
y = -4 / 5 x
-4y = 5x
-4y -5y = 0
<-> 4y + 5y = 0
Persamaan garis lurus yang melalui titik ( 0 , -2 ) dan m = 3/4 adalah . . .?
Penyelesaian :
Diketahui :
Titik garis ( 0 , -2 )
m = 3 / 4
Titik garis ( 0 , -2 )
m = 3 / 4
Ditanya : Persamaan garis = . . .?
Jawab :
Cara 1y = mx + c
y = 3/4 x + ( -2 ) x4
< => 4y = 3x – 8
< = > -3x + 4y + 8 = 0
y = 3/4 x + ( -2 ) x4
< => 4y = 3x – 8
< = > -3x + 4y + 8 = 0
Cara 2y – y1 = m ( x – x1 )
y – ( -2 ) = 3/4 ( x – 0 )
y + 2 = 3/4 x x4
< = > 4y + 8 = 3x
< = > -3y + 4y + 8
Contoh Soal 6y – ( -2 ) = 3/4 ( x – 0 )
y + 2 = 3/4 x x4
< = > 4y + 8 = 3x
< = > -3y + 4y + 8
Tentukan persamaan garis G yang melalui garis ( 0 , 4 ) dan sejajar dengan garis H yang melalui titik pusat koordinat dan titik ( 3 ,2 ) ?
Penyelesaian :
Diketahui :
Titik koordinat ( 0 , 0 ) dan titik ( 3 , 2 )
Titik koordinat ( 0 , 0 ) dan titik ( 3 , 2 )
Ditanya : Persamaan garis G = . . .?
Jawab :
Langkah pertama kita tentukan gradiennya terlebih dahulu , yaitu :
m = y2 – y1 / x2 – x1
m = 2 – 0 / 3 – 0
m = 2/ 3
m = y2 – y1 / x2 – x1
m = 2 – 0 / 3 – 0
m = 2/ 3
Karena Garis G // H , maka gradiennya adalah 2/3 DAN Melalui titik ( 0 , 4 ) , maka persamaan garisnya adalah :
y = mx + c
y = 2 / 3 x + 4 x3
< = >3y = 2x + 12
< = > 3y – 2x – 12 = 0
< = > 2x – 3y + 12 = 0
Contoh Soal 7y = mx + c
y = 2 / 3 x + 4 x3
< = >3y = 2x + 12
< = > 3y – 2x – 12 = 0
< = > 2x – 3y + 12 = 0
Tentukan persamaan garis Z yang melalui titik ( 4 , 5 ) dan ( -5 , 3 ) ?
Penyelesaian :
Diketahui :
Titik A ( 4 , 5 )
Titik B ( -5 , 3 )
Titik A ( 4 , 5 )
Titik B ( -5 , 3 )
Ditanya : Persamaan garis Z = . . .?
Jawab :
Cara 1Langkah pertama yaitu mencari gradien terlebih dahulu :
m = y1 – y2 / x1 – x2
m = 5 – 3 / 4 – ( -5 )
m = 2 / 9
m = y1 – y2 / x1 – x2
m = 5 – 3 / 4 – ( -5 )
m = 2 / 9
Selanjutnya yaitu memasukkan ke dalam rumus :
Persamaan garis melalui titik ( 4 , 5 ) dan bergradien 2 / 9
y – y1 = m ( x – x1 )
y – 5 = 2/9 ( x – 4 )
y – 5 = 2/9x – 8/ 9
y = 2/9 x – 8 / 9 + 5
y = 2/9 x – 8/9 + 45 /9
y = 2/9x – 37 / 9
y – y1 = m ( x – x1 )
y – 5 = 2/9 ( x – 4 )
y – 5 = 2/9x – 8/ 9
y = 2/9 x – 8 / 9 + 5
y = 2/9 x – 8/9 + 45 /9
y = 2/9x – 37 / 9
Cara 2Tanpa mencari gradien, yaitu dengan cara
y – 5 / 3 – 5 = x – 4 / -5 – 4
y – 5 / -2 = x – 4 / -9
-9 ( y – 5 ) = -2 ( x – 4 )
-9y + 45 = -2x + 8
-9y + 2x +45 – 8 = 0
2x – 9y + 37 : 9
< = > 2/9 x – y + 37 / 9
< = > y = 2/9x + 37 / 9
y – 5 / -2 = x – 4 / -9
-9 ( y – 5 ) = -2 ( x – 4 )
-9y + 45 = -2x + 8
-9y + 2x +45 – 8 = 0
2x – 9y + 37 : 9
< = > 2/9 x – y + 37 / 9
< = > y = 2/9x + 37 / 9
Demikian penjelasan mengenai rumus persamaan garis lurus dan beberapa contohnya . Semoga dengan penjelasan di atas, sedikit membantu memecahkan permasalahan dalam mengerjakan soal yang berhubungan dengan persamaan garis lurus .
Inti dari persamaan garis lurus adalah memahami apa itu gradien dan memahami antara titik yang dilalui baik titik pusat koordinat , titik koordinat y ataupun titik koordinat x. Atau jika dilambangkan yaitu titik pusat koordint ( 0 , 0 ) , titik koordinat ( x1 , y1 ) dan ( x2 , y 2 ).
Semoga bermanfaat terima kasih telah mengunjungi blog ini.....

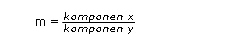
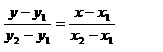
Tidak ada komentar:
Posting Komentar