Pengertian serta Contoh Bilangan Bulat Positif dan Negatif

Hasil gambar untuk pengertian bilangan bulat

Bilangan bulat adalah sistem bilangan yang merupakan himpunan dari semua bilangan (bukan pecahan) yang terdiri dari bilangan bulat negatif{…,-3,-2,-1}, nol {0}, dan bilangan bulat positif{1,2,3,…}. Bilangan bulat merupakan himpunan bagian dari bilangan rasional.

Contoh bilangan bulat positif: 133, 45, 31, 1000

Contoh bilangan bulat negatif: -121, -7, -8, -9, -111

Contoh bukan bilangan bulat: -3½

A. Penyusun Bilangan Bulat

Himpunan semua bilangan bulat dalam ilmu matematika dilambangkan dengan

Ζ atau “Zahlen” (bahasa jerman yang berarti bilangan).

ℤ = Himpunan bilangan bulat

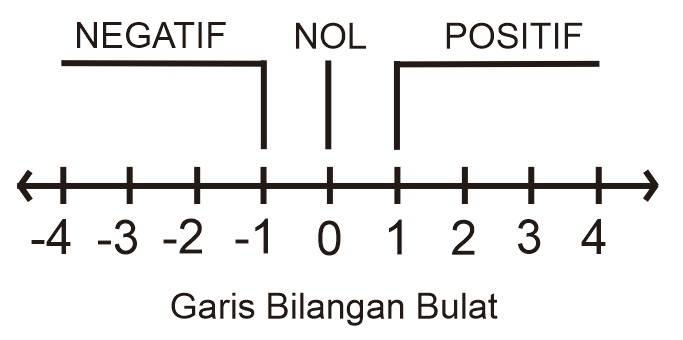
Berikut bilangan bulat pada garis bilangan:

$Bilangan Bulat Negatif$

Bilangan bulat negatif adalah semua bilangan bulat di sebelah kiri garis bilangan yang dibatasi oleh angka nol. Misalnya: -4, -3, -2, -1
Angka Nol

Angka nol adalah digit yang memainkan peranan penting dalam ilmu matematika. Dalam operasi penjumlahan, angka nol menjadi unsur identitas. Ini artinya setiap angka yang dijumlahkan dengan angka nol menghasilkan angka itu sendiri.
Bilangan Bulat Positif atau Bilangan Asli

Bilangan bulat positif adalah semua bilangan bulat di sebalah kanan garis bilangan yang dibatasi oleh angka nol. Misalnya: 1, 2, 3, 4, dst. Bilangan bulat positif dibagi menjadi 2, yaitu bilangan ganjil dan bilangan genap.
- Bilangan Ganjil
  
  Bilangan ganjil adalah bilangan bulat positif yang tidak habis dibagi 2. Misalnya: 1, 3, 5, 7, dst.
- Bilangan Genap
  
  Bilangan genap adalah bilangan bulat positif yang habis dibagi 2. Misalnya: 2, 4, 6, dst.

Catatan: Nol dan bilangan asli membentuk sistem bilangan cacah, {0, 1, 2, 3, …}.

B. Sifat-Sifat Bilangan Bulat

	Penambahan	Perkalian
Tertutup	a + b = adalah bilangan bulat	a × b = adalah bilangan bulat
Asosiatif	a + (b + c) = (a + b) + c	a × (b × c) = (a × b) × c
Komutatif	a + b = b + a	a × b = b × a
Mempunyai unsur identitas	a + 0 = a	a × 1 = a
Setiap bilangan punya invers	a + (−a) = 0
Distributif	a × (b + c) = (a × b) + (a × c)
Tidak ada pembagi nol		jika a × b = 0, maka a = 0 atau b = 0 (atau keduanya)

Keterangan

Tertutup: operasi perkalian dan penjumlahan bilangan bulat menghasilkan bilangan bulat.

Tidak ada pembagi nol: pembagian bilangan bulat dengan nol menghasilkan nilai tidak terdefinisi (∞).

Asosiatif: penjumlahan atau perkalian tiga buah bilangan bulat yang dikelompokkan secara berbeda mempunyai hasil yang sama.

Komutatif: pertukaran letak angka pada penjumlahan dan perkalian bilangan bulat mempunyai hasil sama.

Contoh:

1 + 2 = 2 + 1

3 × 4 = 4 × 3

Unsur identitas: operasi perkalian dan penjumlahan setiap bilangan bulat dengan identitasnya dapat menghasilkan bilangan itu sendiri

Identitas Penjumlahan (0), 7 + 0 = 7
Identitas Perkalian (1), 2 × 1 = 2

Mempunyai Invers: setiap bilangan bulat mempunyai invers terhadap operasi penjumlahan, suatu bilangan bulat yang dioperasikan dengan inversnya menghasilkan unsur identitas penjumlahan.

Contoh:

-7 + 7 = 0; 0 adalah unsur identitas penjumlahan, jadi 7 invers penjumlahannya -7.

Sifat Distributif: suatu penggabungan dengan cara mengkombinasikan bilangan dari hasil operasi terhadap elemen-elemen kombinasi tersebut

Operasi Hitung Bilangan Bulat dan Sifatnya.

Operasi hitung suatu bilangan pada dasarnya terdiri dari operasi penjumlahan (+), Pengurangan (-), Perkalian ( $\times$ ) dan pembagian ( $\div$ ).

Bilangan bulat merupakan bilangan yang terdiri dari bilangan positif, negatif dan nol. Untuk bilangan positif dapat dibaca sesuai dengan simbol yang ada, seperti contohnya 5 (dibaca “Lima”). Tetapi untuk bilangan negatif ada tambahan kata sebelum simbol angka tersebut, contoh -5 (dibaca “Negatif lima”).

Operasi hitung bilangan bulat terdiri dari operasi:
1. Penjumlahan
2. Pengurangan
3. Perkalian
4. Pembagian

1. Penjumlahan
Operasi penjumlahan pada bilangan bulat tidaklah berbeda dengan penjumlahan biasa yang sudah diketahui, untuk mempermudah pemahaman lihat garis bilangan berikut :

Contoh :
a. $1 + 3 = 4$
Karena :
contoh penjumlahan

b. $-4 + 5 = 1$
Karena :
contoh penjumlahan 1

c. $-3 + 2 = -1$
Karena :
contoh penjumlahan 2

2. Pengurangan
Operasi pengurangan pada bilangan bulat tidaklah berbeda dengan pengurangan biasa yang sudah diketahui, untuk mempermudah pemahaman lihat garis bilangan berikut :

Contoh :
a. $5 - 3 = 2$
Karena :
Contoh pengurangan

b. $2 - 6 = -4$
Karena :
Contoh pengurangan 1

c. $-1 - 4 = -5$
Karena :
Contoh pengurangan 2

3. Perkalian
Untuk operasi perkalian dalam bilangan bulat sama dengan operasi perkalian biasa, hanya ada hal yang perlu diperhatikan, bahwa :
a. Jika bilangan positif dikalikan dengan bilangan positif maka hasilnya positif.
Contoh :
$2 \times 4 = 8$
$4 \times 9 = 36$

b. Jika bilangan positif dikalikan dengan bilangan negatif maka hasilnya negatif.
Contoh :
$-3 \times 4 = -12$
$-5 \times 3 = -15$

c. Jika bilangan negatif dikalikan dengan bilangan positif maka hasilnya negatif.
Contoh :
$2 \times -9 = -18$
$3 \times -7 = -21$

d. Jika bilangan negatif dikalikan dengan bilangan negatif maka hasilnya positif.
Contoh :
$2 \times 7 = 14$
$4 \times 4 = 16$

4. Pembagian
Untuk operasi pembagian dalam bilangan bulat sama dengan operasi pembagian biasa, hanya ada hal yang perlu diperhatikan, bahwa :
a. Jika bilangan positif dibagi dengan bilangan positif maka hasilnya positif.
Contoh :
$18 \div 3 = 6$
$28 \div 7 = 4$

b. Jika bilangan positif dibagi dengan bilangan negatif maka hasilnya negatif.
Contoh :
$21 \div -3 = -7$
$36 \div -3 = -12$

c. Jika bilangan negatif dibagi dengan bilangan positif maka hasilnya negatif.
Contoh :
$-33 \div 3 = -11$
$-18 \div 2 = -9$

d. Jika bilangan negatif dibagi dengan bilangan negatif maka hasilnya positif.
Contoh :
$-9 \div -3 = 3$
$-12 \div -2 = 6$

Operasi hitung berjajar
Pada operasi hitung berjajar ada beberapa hal yang perlu diperhatikan, yaitu sbb:
a. Bila ada tanda operasi hitung berjajar penjumlahan (+) dan pengurangan/negatif (-), maka dapat diartikan bahwa operasi tersebut adalah operasi pengurangan (-)
misal : $5 + (- 3)$ artinya $5 - 3 = 2$

b. Bila ada tanda operasi hitung berjajar pengurangan/negatif (-) dan penjumlahan (+), maka dapat diartikan bahwa operasi tersebut adalah operasi pengurangan (-)
misal : $5 - (+ 4)$ artinya $5 - 4 = 1$

c. Bila ada tanda operasi hitung berjajar pengurangan/negatif (-) dan pengurangan/negatif (-), maka dapat diartikan bahwa operasi tersebut adalah operasi penjumlahan (+)
misal : $5 - (- 3)$ artinya $5 + 3 = 8$

Sifat operasi hitung bilangan bulat
1. Sifat Komutatif
Pada bilangan bulat terdapat sifat komutatif atau bisa dikatakan pertukaran. sifat ini hanya berlaku pada operasi penjumlahan dan perkalian.
Contoh :
$2 + 7 = 9$ , sama dengan $7 + 2 = 9$
$3 \times 9 = 27$ , sama dengan $9 \times 3 = 27$

2. Sifat Asosiatif
Sifat asosiatif dikenal juga dengan sifat pengelompokan. Sifat ini juga hanya berlaku pada operasi penjumlahan dan perkalian.
Secara umum sifat asosiatif dapat dinyatakan dalam :
$(a + b) + c = a + (b + c)$ untuk operasi penjumlahan
$(a \times b) \times c = a \times (b \times c)$ untuk operasi perkalian.

Contoh :
$(2 + 4) + 3 = 9$ sama dengan $2 + (4 + 3) = 9$
$(2 \times 3) \times 5 = 30$ sama dengan $2 \times (3 \times 5) = 30$

3. Sifat Distributif
Sifat distributif dalam bilangan bulat disebut juga sifat penyebaran.
Sifat distributif pada bilangan bulat ada dua yaitu :
a. Sifat distributif perkalian terhadap penjumlahan dengan bentuk umum (a + b) \times (a + c) = a \times (b + c)
Contoh :
(2 + 4) \times (2 + 6) = 2 \times (4 + 6)
karena pada (2 + 4) \times (2 + 6) terdapat angka 2 sebagai pengali yang sama sehingga bisa di sederhanakan menjadi 2 \times (4 + 6)

b. Sifat distributif perkalian terhp pengurangan dengan bentuk umum (a – b) \times (a – c) = a \times (b – c)
Contoh :
(9 – 5) \times (9 – 3) = 9 \times (5 – 3)
karena pada (9 – 5) \times (9 – 3) terdapat angka 9 sebagai pengali yang sama sehingga bisa di sederhanakan menjadi 9 \times (5 – 3)

BENTUK AKAR

Bentuk akar merupakan akar dari suatu bilangan yang hasilnya bukan bilangan rasional atau merupakan bilangan irasional. Bentuk akar merupakan bentuk lain untuk menyatakan bilangan berpangkat. Bentuk akar termasuk dalam bilangan irasional, yakni bilangan yang tidak dapat dinyatakan dengan pecahan a/b, a dan b bilangan bulat a dan b ≠ 0. Bilangan bentuk akar merupakan bilangan yang terdapat di dalam tanda √ disebut tanda akar. Beberapa contoh bilangan irasional dalam bentuk akar adalah √2, √6, √7, √11 dan lain-lain. Sedangkan √25 bukan bentuk akar hal ini karena √25 = 5 (5 adalah bilangan rasional).

Seperti halnya bilangan berpangkat, bilangan bentuk akar juga memiliki sifat-sifat tertentu. Sifat-sifat ini akan memudahkan dalam melakukan operasi aljabar yang melibatkan bentuk akar.

MERASIONALKAN BENTUK AKAR

Untuk memudahkan penggunaan bentuk akar dalam operasi aljabar, bentuk akar dituliskan dalam bentuk yang paling rasional (sederhana). Cara merasionalkan bentuk akar harus memenuhi syarat-syarat tertentu. Syarat-syarat tersebut adalah sebagai berikut:

Selanjutnya, bagaimana caranya merasionalkan penyebut pecahan dalam bilangan bentuk akar? Merasionalkan penyebut pecahan bilangan bentuk akar itu artinya, mengubah penyebut pecahan yang berbentuk akar menjadi bentuk rasional (sederhana). Cara untuk merasionalkan penyebut pecahan yaitu dengan mengalikan pembilang dan penyebut pecahan tersebut dengan bentuk akar yang sekawan dari penyebut tersebut.

Ada tiga cara merasionalkan penyebut bentuk pecahan bentuk akar, yaitu :

OPRASI ALJABAR BENTUK AKAR

Penjumlahan dan Pengurangan Bentuk Akar

Variabel pada bentuk akar dapat dijumlahkan atau dikurangkan jika sejenis dan memenuhi sifat seperti berikut:

Perkalian Bentuk Akar

Perkalian variabel pada bentuk akar memenuhi sifat seperti berikut:

Pembagian Bentuk Akar

Selain penjumlahan, pengurangan dan perkalian, variabel pada bentuk akar dapat berupa pembagian yang memenuhi sifat seperti berikut:

Nah, supaya kamu lebih paham coba kerjakan contoh soal di bawah ini ya

Jawab:

Bilangan Berpangkat

Apabila ada sebuah bilangan a dikalikan sebanyak n kali, maka bisa dikatakan sebagai a pangkat n atau aⁿ
Bilangan berpangkat dapat dinyatakan dengan rumus:

an=a×a×a×a...sebanyak n kali

dimana:
a=bilangan basis (dasar)
n=bilangan pangkat (eksponen)

Jenis-jenis Bilangan Berpangkat:

Bilangan Berpangkat Bulat Positif
Bilangan yang disederhanakan dari hasil perkalian dengan basis bilangan yang sama

Contoh Bilangan Pangkat Bulat Positif:
•

53
=5×5×5=125
•

24
=2×2×2×2=16
Bilangan Berpangkat Nol

an

an

=an−n=
a0
=1

Contoh Bilangan Pangkat Nol:
•

30
=1
•

52
:
52
=
52−2
=
50
=1
•

34

34

=1

Kelipatan Dan KPK Suatu Bilangan Cacah

Kelipatan suatu bilangan cacah

Kelipatan suatu bilangan cacah diperoleh dengan cara mengalikan bilangan tersebut dengan semua anggota bilangan cacah. Hal ini dapat dilihat sebagai berikut:
*Kelipatan 2 pada bilangan cacah adalah hasil kali bilangan 2 dengan semua anggota bilangan cacah dan ditulis:
K2 = 2 x 0, x 1, 2 x 2, 2 x 3, dan seterusnya.
himpunan K2 = {0, 2, 4, 6, . . .}.
*Kelipatan 3 pada bilangan cacah adalah hasil kali bilangan 3 dengan semua anggota bilangan cacah dan ditulis:
K3 = 3 x 0, 3 x 1, 3 x 2, 3 x 3, dan seterusnya.
Himpunan K3 = { 0, 3, 6, 9, . . .}.
*Kelipatan 4 = K4 = 4 x 0, 4 x 1, 4 x 2, 4 x 3, ... = 0, 4, 8, 12
Himpunan K4 = {0, 4, 8, 12, . . .}
*Himpunan kelipatan persekutuan antar bilangan cacah.
Himpunan kelipatan persekutuan (HKP) antar bilangan cacah merupakan dua himpunan kelipatan yang tidak saling lepas. HKP dari m dan n ditulis Km ≖Kn.

Kelipatan persekutuan terkecil (KPK) antar bilangan cacah
Kelipatan persekutuan terkecil dari dua atau lebih bilangan cacah adalah bilangan asli terkecil dari himpunan persekutuan bilangan cacah itu.Kelipatan persekutuan terkecil dari dua bilangan disingkat KPK. Untuk membahas masalah ini mari kita perhatikan contoh berikut ini:
Himpunan kelipatan 2 adalah K2 = {0, 2, 4, 6, 8, . . .}
Himpunan kelipatan 3 adalah K3 = {0, 3, 6, 9, 12, . . .}
Himpunan kelipatan persekutuan (KPK) dari 2 dan 3 adalah
K2 ≖K3 = {0, 6, 12, 18, . . .}. Bilangan asli terkecil dari K2 ≖K3 adalah 6, maka KPK dari 2 dan 3 adalah 6.

Penggunaan KPK dan FPB
Dalam kehidupan sehari-hari kadang kita menjumpai soal-soal cerita yang harus menggunakan KPK dan FPB untuk menyelesaikannya.

Matematika Kls 8

Rabu, 27 Februari 2019